Loading [MathJax]/jax/output/CommonHTML/jax.js
+ - 0:00:00
Notes for current slide
Notes for next slide

Measurement bias

What If: Chapter 9

Elena Dudukina

2021-03-03

1 / 16

9.1 Measurement bias

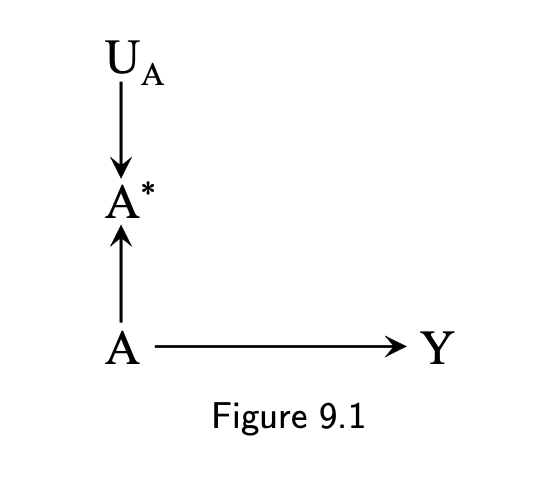
  • Independent errors
2 / 16

9.2 The structure of measurement error: dependent misclassification

  • No single structure (unlike for confounding or selection bias)
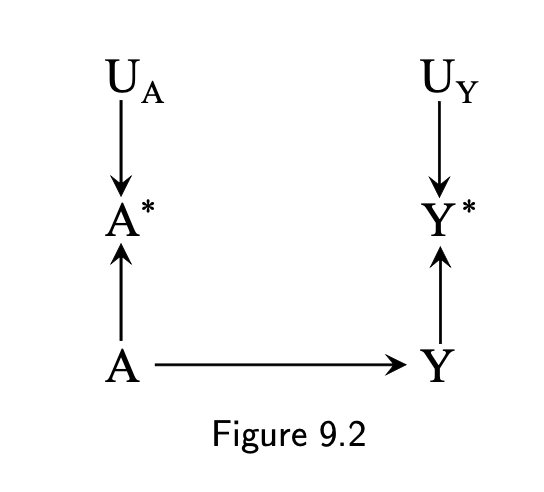
  • Independence and nondifferentiality
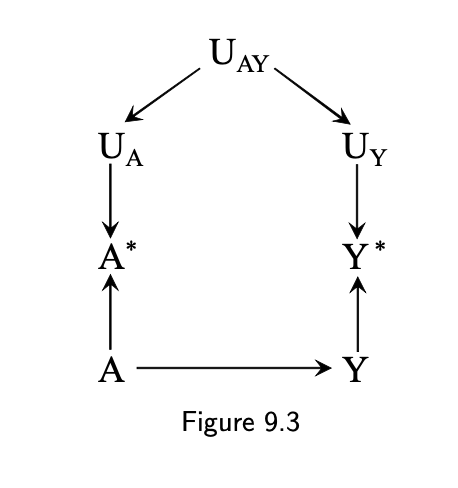
  • Dependent errors
3 / 16

9.2 The structure of measurement error: differential misclassification

  • Differential misclassification
  • Outcome ➵ how exposure was measured (recall bias)
  • Exposure ➵ how outcome is measured (detection bias)
  • Independent errors
  • Differential misclassification
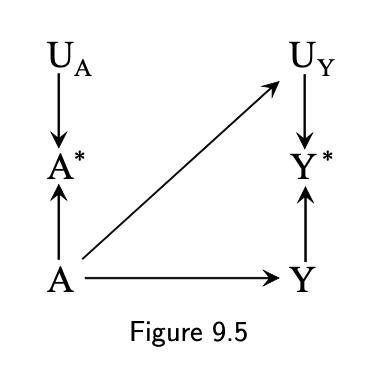
4 / 16

9.2 The structure of measurement error: dependent & differential misclassification

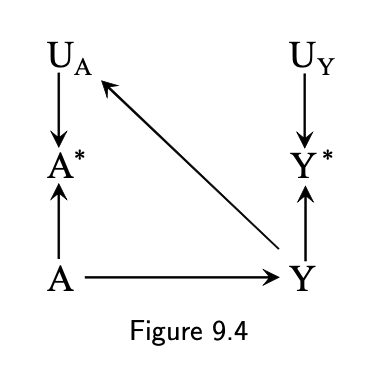
  • Dependent
  • Outcome ➵ how exposure was measured (recall bias)
  • Exposure ➵ how outcome is measured (detection bias)
  • Independent errors
  • Differential misclassification
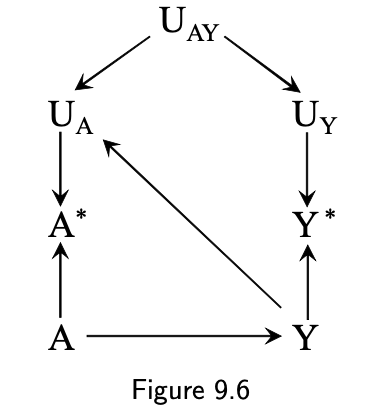
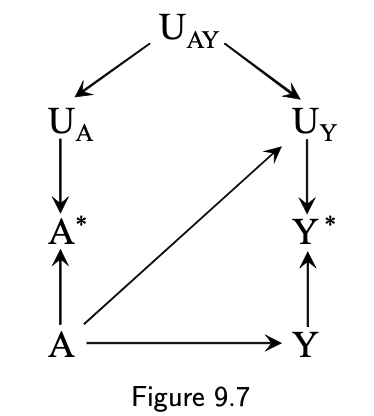
5 / 16

Fine point 9.1

  • Measurement error will result in bias
  • Except if A and Y are unassociated and the measurement error is independent and nondifferential
  • "The magnitude of the measurement bias depends on the magnitude of the measurement error"
  • "Causal diagrams do not encode quantitative information, and therefore they cannot be used to describe the magnitude of the bias"
6 / 16

9.3 Mismeasured confounders

  • A: drug use
  • Y: liver disease
  • L: hepatitis history via questionnaire
  • the backdoor A ⬅️ L ➡️ Y cannot be blocked by conditionning on L*

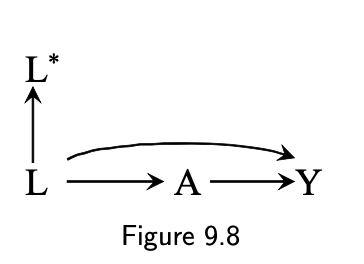
7 / 16

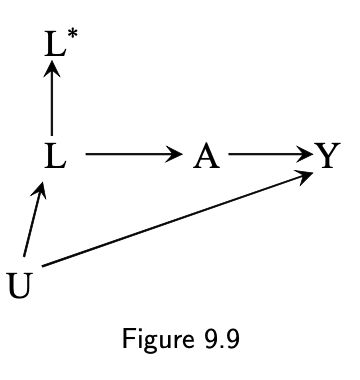
9.3 Mismeasured confounders

  • A: drug use
  • Y: liver disease
  • L: hepatitis history via questionnaire
  • the backdoor A ⬅️ L ⬅️U ➡️Y cannot be blocked by conditionning on L*
8 / 16

9.3 Mismeasured confounders

  • Mismeasurement of confounders may also lead to appearance of effect modification (EMM)
  • If L=0 and L=1 strata differently report L∗, stratification by L∗ would produce appearance of EMM
9 / 16

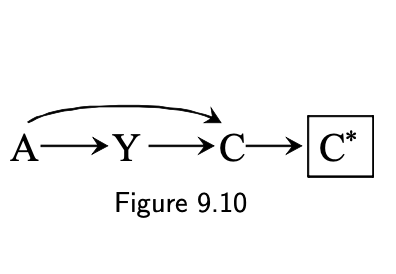
9.3 Conditioning on mismeasured collider

  • Selection bias
10 / 16

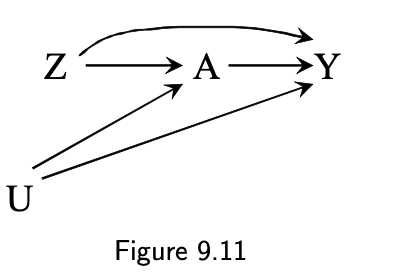
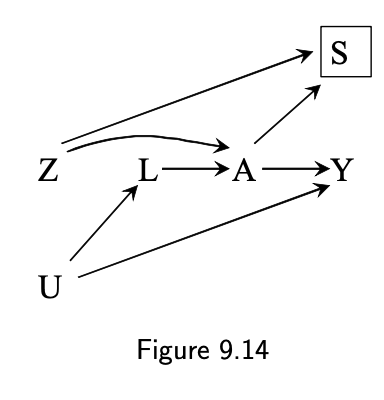
9.4 Intention-to-treat effect: the effect of a misclassified treatment

  • Z: randomization
  • A: treatment
  • Y: outcome
  • U: unmeasured
  • Z ➡️ Y arrow is present when there is unblinding or allocation concealment failure
  • exclusion restriction (assumption: no arrow from Z to Y)
  • Effect of Z is intention-to-treat effect (ITT)
11 / 16

9.5 Per-protocol effect

  • Causal effect of the treatment itself and not of randomization to treatment level
  • Lack of exchangeability between A=1 and A=0
  • Back to observational epidemiology realm
12 / 16

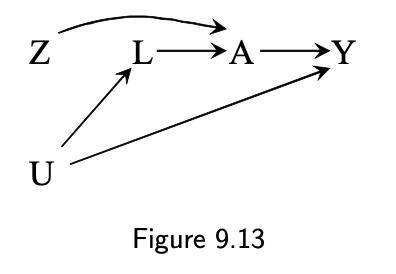
Fine point 9.2

As-treated vs per protocol

As-treated

  • Y=1 in those A=1 vs Y=1 in those A=0 regardless of Z
  • Confounded (9.11 & 9.12)
  • Feasible and estimable given L (9.13)

Per protocol

  • Only those who have adhered to the study protocol (A=Z)
  • Y=1 in those Z=1 vs Y=1 in those Z=0
  • ITT in per-protocol population
  • Selection bias

13 / 16

ITT

ITT is a lower bound for per-protocol effect

  • ITT is closer to null (conservative)
    • Not in safety studies
  • ITT is null if there is no effect
  • ITT assumes monotonicity (same direction of the effect in all individuals)
14 / 16

Per protocol

  • Time-varying
  • Report both ITT and per-protocol effects
    • trade-off between bias due to potential unmeasured confounding vs misclassification of exposure
  • IV approach
  • Adjustment approach
15 / 16

References

Hernán MA, Robins JM (2020). Causal Inference: What If. Boca Raton: Chapman & Hall/CRC (v. 31jan21)

16 / 16

9.1 Measurement bias

  • Independent errors
2 / 16
Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow